순환소수 문제는 반복적으로 풀어봄으로써 익숙해지고 수월하게 풀 수 있습니다. 무엇이든 엉덩이로 공부하는 것이죠.

-------------------------
풀이 과정
먼저, 분수를 소수로 나타낸다. 10 ÷ 11 을 계산하면, "0.90909090909....."이므로, 순환되는 숫자는 '9'와 '0'이다.
※ 따라서, 순환마디 숫자의 갯수는 2개 - 정답은 ②번

-------------------------
풀이 과정
순환되는 숫자를 먼저 찾아 보자. 순환되는 숫자는 '2' '4'와 '7'과 '1'이다. 물론 50번째까지 모두 기록해서 꼼꼼히 확인하여도 되겠지만, 3의 배수대로 순환마디의 숫자가 진행됨을 이용해 보자.
그러면 50 ÷ 3 = 16 ... 나머지 2가 된다. 즉 48번째의 숫자는 '1'이라는 말이다. 그렇다면 49번째 숫자는 순환되는 숫자의 처음으로 돌아가 '2' '4'가 되고 50번째는 '7'이 된다.
※ 따라서 50번째 숫자는 "7"이다.
* 20200618목 : #중2병님 께서 말씀하신 대로 숫자 '4'를 '2'로 잘못 기록하여 수정합니다.


-------------------------
풀이 과정
앞선 두 문제의 혼합형으로 생각해 볼 수 있겠다.
먼저 주어진 분수를 소수로 나타내어 보자. 2 ÷ 11 = 0.18181818181.... 이다. 이 경우에는 소수점 아래 홀수번째의 숫자는 '1', 소수점 아래 짝수번째의 숫자는 '8'이다.
※ 소수점 아래 22번째 자리의 숫자는 짝수번째 숫자이고 '8'이 되며, 소수점 아래 33번째 자리의 숫자는 '1'이다. 그러므로 a = 8, b = 1이고, "a + b = 9" 이다.

-------------------------


-------------------------
풀이 과정
주어진 각 항목들을 분수로 고쳐 보면 된다.
유의할 점은, 소수점 이하에 순환소수가 아닌 자릿수가 몇 개인가를 확인하는 것이다.
①과 ②와 ③은 소수점 이하에 순환소수가 아닌 자릿수가 없다. 그러므로 분수로 나타낼 때 무조건 분모가 "9"가 된다.
④과 ⑤는 소수점 이하에 순환소수가 아닌 자릿수가 각각 소수점 첫번째 자리이다. 그러므로 소수점 이하에 순환소수가 없는 갯수만큼 분모에 "0"을 늘려 주므로, ④과 ⑤는 무조건 분모가 "90"이 된다.
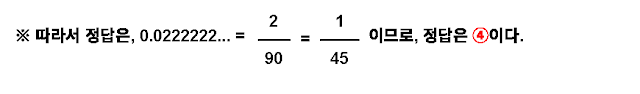
댓글